Start | Grundlagen | Wechselstromtechnik | Nachrichtentechnik | Digitaltechnik | Tabellen | Testaufgaben | Quiz | PDF-Dateien
AnzeigeSchwingkreis
Schaltet man eine Spule (Induktivität) und einen Kondensator (Kapazität) zusammen, so entsteht ein Schwingkreis. Die Zusammenschaltung kann entweder in Form einer Reihenschaltung oder in Form einer Parallelschaltung erfolgen.
Wird an solch eine Schaltung kurzfristig eine Spannung angelegt, dann lädt sich der Kondensator bis maximal auf den Spannungswert der Spannungsquelle auf. Schaltet man dann die Spannung wieder ab, dann entlädt sich der Kondensator über die Spule wieder. Durch die Spule lädt sich der Kondensator erneut mit entgegengesetzter Polarität auf. Dieser Vorgang wiederholt sich mehrmals, wobei die Spannungshöhe aufgrund der im Schwingkreis vorhandenen Wirkwiderstände immer geringer wird. Es entsteht auf diese Weise eine gedämpfte Schwingung.
Ein Sonderfall tritt dann auf, wenn der induktive und der kapazitive Blindwiderstand gleich groß sind und sich damit gegenseitig aufheben. In diesem Fall hat der Schwingkreis nur noch einen Wirkwiderstand. Diesen Fall bezeichnet man als Resonanz.
Die Frequenz bei der dies der Fall ist wird als Resonanzfrequenz f0 bezeichnet.
XL = XC |
Im Resonanzfall sind der induktive Blindwiderstand XL und der kapazitive Blindwiderstand XC gleich groß. | |
 |
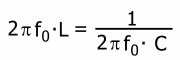setzt man für XL und XC die entsprechenden Gleichungen ein und löst anschließend diese Gleichung nach f0 auf so erhält man: | |
|
Resonanzfrequenz des Schwingkreises |
Anzeige
Unsere Buchtipps zur Elektrotechnik
Impressum | Datenschutz